How well do T Levels – the new vocational alternative to A levels – prepare students to study Engineering? Do they provide an adequate grounding in maths necessary to succeed? Is the mathematical content in an Engineering T Level as good as a Maths A level? Or, given that it’s learned in an applied setting, is it perhaps better?
These were some of the questions that the EPC set out to answer in an initiative prompted by discussions with the Department for Education, the Royal Academy of Engineering and the Engineering Council. The research has been conducted by Dr Mariam Makramalla, under the direction of a steering group chaired by Prof Chris Atkin CEng FREng FRAes.
Dr Makramalla’s report – published below in a draft form, exclusively for EPC members – provides a guide to what T levels are, the mathematical content you can expect a student to have covered, how that compares with A level Maths content, and in what contexts different level 3 qualifications provide the best foundation for studying Engineering. The aim is to better inform the admissions policies of engineering departments when it comes to making offers to T level students.
The draft of this report will be launched and discussed at a webinar on Tuesday 30th January 2024 (register here). The report may be amended to reflect feedback and discussion at that event and following and a final version will be made public in February 2024.
This report is the first in our Maths for Engineering project, which is generously supported by the Gatsby Charitable Foundation. The project will go on to conduct a wider comparative study of the whole landscape of level 3 qualifications including A levels, Scottish Highers, the Welsh Baccalaureate, BTECs, the International Baccalaureate and so on. Those findings will be published later in 2024.
An embargoed PDF version of the report can be downloaded from the link below. This is not for wider distribution as it may be amended to reflect feedback about how it can be as helpful as possible to Engineering departments.
We would be grateful for your feedback about this report before a final version is published. Please complete this short survey.
1. Introduction
This report has been prompted by the current transition from BTECs (which are almost all being defunded) to T Level qualifications.
In the following, we scope the coverage of mathematics in T levels, both on a curricular and an assessment level. We present this following concerns raised regarding the mathematics entry level requirements for Engineering higher education and in the hope of supporting a better informed approach to Engineering admissions.
2. What are T levels?
Intended as an alternative route to A levels or the direct entry into apprenticeship-based jobs, T levels are a two-year programme that targets 16-19 year-old students. The T level programme is designed based on an interdisciplinary learning approach, in which sciences and mathematics are integrated in complex challenges that students must understand and tackle.
One T Level is intended to be equivalent to three A levels. Students interested in pursuing an engineering-oriented study programme can undertake one of the following specialisms:
- Onsite Construction;
- Building Services Engineering;
- Design & Development for Engineering & Manufacturing;
- Maintenance, Installation & Repair;
- Engineering, Manufacturing & Processing Control.
Additionally, students can also choose to concentrate on the following non-engineering specialisms: Management & Administration; Agriculture, Land Management & Production; and Animal Care & Management (to be launched in Autumn 2024).
2.1 How are T Levels assessed?
The assessment structure of T levels is made up of
1) Exams
Students sit standardised closed book exams in the following fields: (a) Paper 1: Maths & Sciences; (b) Paper 2: Engineering Studies. Written examinations are made available periodically at set assessment periods. Exams are assessed based on a pre-set rubric and are marked by a set of external examiners. A rigorous quality assurance process is administered, whereby exam papers are double-marked and cross-checked at several levels across the assessment committee.
2) Projects
Students undertake employer-set projects that are composed of 4 main tasks; namely (a) a research task, (b) a reporting task, (c) a design task and (d) a presentation task.
Employer-set projects are made up of scenario-based challenges. Students analyse a given problem, research different solutions, report on their problem statement, conduct problem analysis and research solutions. Students also design a prototype of a gadget that is presented as a solution to the presented problem. Finally, students record a presentation outlining their problem-solving process.
The project-based assessment is centrally administered. It is not conducted by the employers themselves. The project-based assessment unit takes place over one practical assessment week, whereby clear milestones are outlined for each student. Research papers and reports that result from the practical assessment are assessed via a centralised unit of external assessors. The design task is either CAD-based or paper-based. It gets scanned and assessed according to a rubric that is predefined by a committee of external assessors. Student presentations are recorded and tthe recordings are also marked according to a pre-set rubric.
3. T Level qualifications & higher education entry level requirements in Engineering
Discussions with representatives of different higher education admissions stakeholders in the engineering field revealed that there are no set criteria for entry level mathematics. On the whole, the landscape of UK Engineering higher education admissions can be depicted as lying on a two-dimensional spectrum, presented by the below matrix (Figure 1).
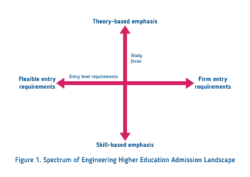
It is important to consider the matrix in Figure 1 as a spectrum rather than a fixed structure. In other words, there is no engineering degree programme that would focus solely on skill development. Similarly, there is no degree that is purely theory-based. In the same way, the mathematics knowledge and skill entry requirements also need to be seen as lying on a spectrum that extends between firm and flexible criteria.
Based on this navigational framework, we have interviewed more than 20 stakeholders that have situated themselves in different quadrants of this spectrum. Those stakeholders adopted different views of T Level Mathematics for the purpose of admission to an engineering degree.
4. Higher education entry requirements in Engineering: Mathematics T Level mapping
In sections 4.1 to 4.4, we have presented the findings of a multi-stranded mapping process between Engineering HE entry level requirements in Mathematics (across the spectrum in Figure 1) and T Level Mathematics knowledge and skill sets. We distinguish between a mapping conducted at curricular level and mapping conducted at assessment level.
4.1 T Level Mathematics curricular content mapping
In this section, we focus solely on mapping the coverage of mathematics content when compared to Mathematics A levels. We map this against firm entry requirements of Engineering schools that could be classified as lying on the theory-oriented end of the concentration spectrum in Figure 1 (see Section 3). Table 1 below presents a comparative account of the overarching content areas covered in T levels and expected at firm entry level theory-based engineering schools.
Table 1. Overarching mapping (More details in Appendix)
| T Level Mathematics | A Level Mathematics | Firm entry level expectations |
| Number | Numerical Methods | Numbers & Complex Numbers |
| Algebra | Algebra & Coordinate Geometry | Algebra & Cartesian Geometry |
| Logs and Exponentials | Exponentials and Logarithms | Exponentials & Logarithms |
| Sequences & Series | Sequences & Series | Sequences & Series |
| Calculus | Differentiation & Integration | Differentiation & Integration |
| Functions (not covered) | Functions | Functions |
| Trigonometry | Trigonometry | Trigonometry |
| Vectors & Matrices | Vectors | Matrices |
| Statistical Analysis | Statistical Sampling, Data presentation & Interpretation, Probability, Statistical Distribution, Statistical hypothesis & testing | Statistics |
Table A (see Appendix) presents a detailed content area map that has been designed by admissions tutors at Leicester College. The detailed map presents a comparative account of learning outcomes across the two comparator qualifications (T levels and A levels). These are mapped against theory-based firm entry level requirements at Engineering departments (see Figure 1 in Section 3). Academic staff acknowledge the presence of mathematical knowledge area gaps when mapping the content covered in A Levels compared to the content covered in T levels. Discussions with stakeholders in HE admissions revealed ongoing concerns regarding the level of content mathematical knowledge currently expected at the entry level of Engineering departments and whether this was practically applicable in the engineering industry today and therefore potentially less necessary as a requirement.
4.2 T Level Mathematics curricular skills mapping
T Level instruction happens over three different pedagogical components; namely
- a core classroom-based component,
- an occupational component, and
- an industry placement component (Figure 2).
The first (core classroom) component is delivered in year 1. Students learn different concepts and theories relating to Mathematics and Sciences. Table 1 (see Section 4.1 T Level Mathematics curricular content mapping) presents the overarching content areas covered in mathematics. The teaching adopts an interdisciplinary approach, whereby the teaching of Mathematics is blended with the applications in the sciences.
The second (occupational) component is based on the chosen student specialism (see specialisms in section 2). Specialism-specific instruction takes place either in the classroom or in the designated workshop.
The third (industry placement) component requires students to complete 45 placement days in the industry relevant to the specialism of choice. Students can complete the 45-day (315-hour) placements in one block. Students could also choose to spread the required placement hours over the course of the two study years (subject to their arrangements offered by their provider and the employer).
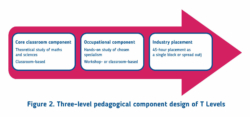
Resulting from this three-level pedagogical design T level graduates are equipped with (1) complex problem-solving skills; (2) practical contextualised engineering skills, (3) communication skills, (4) interdisciplinary learning skills, (5) hands-on application skills and (6) critical thinking skills.
When mapping these skills against the entry requirements in the Engineering HE admissions, it becomes clear that Engineering departments (with firm or flexible entry requirements) that run a study programme which is more practice-oriented value students who have acquired the above entry level skill set. Theory-oriented Engineering departments, on the other hand, have one application-oriented entry requirement (Application of Mathematics), which may be screened during in-person interviews at entry level (if they conduct interviews). The entry level interview focuses on logical thinking and communication skills acquired by the applicant at entry level.
4.3 T Level Mathematics assessment content mapping
The core classroom component (see Figure 2 in section 4.2) is assessed through a centrally governed standardised examination process. Sciences and Mathematics are tested in one examination and the chosen Engineering specialism is tested in a separate one. Students have the choice to complete their written assessment either at the end of the first or at the end of the second year.
Table 1 shows the over-arching content areas that get assessed in the theoretical exam for mathematics. Examinations are centrally designed and assessors mark each exam paper based on a given standard rubric.
4.4 T Level Mathematics assessment skill mapping
The second component (occupational skills) is assessed through an externally drafted practical examination (see Figure 2 in section 4.2). The examination is challenge-based. It introduces the student to a scenario from their chosen specialism. Students need to use the knowledge and skills acquired to address different milestones of the challenge. The scenarios are also referred to as ‘employer set projects’. They are not set by the employers themselves but are rather set by the awarding organisation.
Employer set projects extend over a limited time frame. There are four main tasks that a student needs to engage with throughout this practical assessment. These are: (1) a research task, (2) a reporting task, (3) a design task and (4) a presentation task. In this way, the student goes through all stages of the Engineering Design Cycle to solve the problem at hand.
The employer set projects are externally assessed by a committee of examiners. Assessment is based on a given rubric. The examination committee is monitored by a hierarchy of examination assessors to ensure the quality and consistency of the assessment process across various employers.
5. Conclusion: What should universities do?
Depending on their positioning on the landscape framework presented in Figure 1 (see section 3), Engineering departments are more/less likely to take up T level graduates. Based on interviews held with stakeholders, Table 2 below presents a potential response from stakeholders across the spectrum presented in Figure 1.
Table 2. Higher Education Engineering Admission Responses to T Levels
| Positioning on Landscape | Expected Response | Recommended Action |
| Theory-based focus with firm entry requirements | T Level content level of mathematics would be deemed as unsatisfactory. T level graduates stand fewer chances to study in this sector. | Interviews revealed that this category of engineering schools would expect T level graduates to study A level Mathematics alongside their T Level Mathematics.
Interviews with T level instructors revealed this option is not normally possible. One recommendation would be for this sector to consider collaborating with Leicester College (see Appendix) who have designed a ‘bridging course’ to be offered to T level graduates prior to their entry into the HE sector in Engineering. |
| Theory-based focus with flexible entry requirements | The nature of the flexible entry requirements should mean that T level graduates would be capable of admission to Engineering departments without impediment. | At university level, students follow a theoretical Mathematics course during their first year to ensure all students have the same foundational level of knowledge. |
| Practice-based focus with firm entry requirements | Engineering departments have re-envisioned their entry level assessments to focus more on an in-depth examination of student-acquired skill set.
Stakeholders report a higher than average likelihood of accepting T Level students. |
At university level, students follow a theoretical Mathematics course during their first year to ensure all students have the same foundational level of knowledge. |
| Practice-based focus with flexible entry requirements | Flexible entry requirements allow T Level students to enter. | Interviews with T Level students indicated that this type of Engineering school was their preference when it comes to higher education.
A practice-based orientation of studying Engineering aligns more with their study of the T levels. Flexible entry requirements would enable them to explore HE options with a higher chance of admission. |
Appendix
Attached to this report is a curricular level mapping table that has been created by colleagues at Leicester University. It presents the gaps in terms of content area coverage between T Levels and A Levels. Leicester College is currently in the process of designing a ‘bridging course’ that T level students could take, so that their T level students would be more directly equivalent to their A level counterparts when it comes to Mathematics.
Acknowledgements
The Maths for Engineering initiative is funded by the Gatsby Charitable Foundation. We would like to express our gratitude to them for their generous support.
The Engineering Professors’ Council Maths for Engineering Advisory Group was created to oversee this research. We would like to express our sincere thanks to the Advisory Group for their commitment, expertise and generosity with their time.
Advisory Group Membership
- Chair: Prof Chris Atkin, University of East Anglia and former Chair of the Engineering Council
- Stylli Charalampous, Royal Academy of Engineering
- Stella Fowler, Engineering Professors’ Council
- Dr Paul Greening, Coventry University
- Prof Georgina Harris, Arden University
- Prof Catherine Hobbs, University of Bristol
- Dr Rachel Long, University of the West of England Bristol
- Research Lead: Mariam Makramalla, Engineering Professors’ Council
- Dr Rhys Morgan, Royal Academy of Engineering
- Prof Abel Nyamapfene, University College London
- Prof Geoff Parks, University of Cambridge
- Johnny Rich, Engineering Professors’ Council
- Prof Colin Turner, University of Ulster
We would also like to express our sincere thanks to: Rhys Morgan and other colleagues at the Royal Academy of Engineering; Paul Bailey from the Engineering Council; Jenifer Burden, Faye Riley, Terri Ashton and other colleagues at the Gatsby Charitable Foundation; the Executive Team of the EPC.
We would be grateful for your feedback about this report before a final version is published. Please complete this short survey.




